近日,广东工业大学计算机学院数据挖掘与信息检索实验室(DMIR)团队的论文“Transferable Time-Series Forecasting under Causal Conditional Shift” 被机器学习领域的国际顶级学术期刊IEEE Transactions on Pattern Analysis and Machine Intelligence (TPAMI) 接收。TPAMI期刊由国际电气和电子工程师协会(IEEE)创办,是人工智能领域的顶级期刊,也是中科院SCI一区TOP期刊,影响因子为23.6。下面带来该论文的详细解读。

1. 针对时间序列预测的领域自适应
在时间序列预测任务中,如何从一个环境训练的模型迁移到另一个环境并且保证模型性能是一个难题。现有的方法大多借鉴了经典领域自适应的思路并且平推到时序数据上,但是这些方法通常依赖于协变量偏移假设。而在时序数据中,时序的依赖(例如,简单的一阶马尔可夫依赖)使得协变量偏移假设其实是难以成立。因此如何合理地设计出一个针对时间序列预测的迁移模型成为了一个迫切的需求。
2. 为什么时间序列数据可以预测
在探索如何设计一个针对时间序列预测的领域自适应模型之前,我们不妨先思考一个问题:为什么时间序列可以预测?其实我们可以从生活经验中获得答案,例如在农业生产中,我们常常听到” 瑞雪兆丰年”;在气象预测中,我们也有”蚂蚁搬家蛇过道,不久就有大雨到。”这些生活经验告诉我们,我们可以得知,时间序列数据之所以可以被预测,是因为历史出现过的模式(pattern)是可以复制的。类似的,在机器学习中,我们可以通过发现时间序列数据背后的模式来进行预测,而在本文中,我们认为格兰杰因果结构便是这样的一种模式。
3. 因果条件偏移假设
在讨论完时间序列可以通过格兰杰因果结构进行预测后,我们进一步思考不同领域的时间序列中,什么是可以迁移的?即什么是变的,什么是不变的。由于上一节中我们提到了,我们可以通过格兰杰因果结构来预测时间序列,因此我们不妨假设,不同领域的格兰杰因果结构是不变的,于是我们便有本文的核心假设:因果条件偏移假设(如下图所示)。

在这个假设中,我们允许条件分布是随着领域变化而变化的,但是不同领域的因果结构是稳定不变的。
4. 格兰杰因果对齐模型
在因果条件偏移假设,我们假设格兰杰因果结构是稳定的。接下来,为了设计出时间序列预测的自适应模型,我们还需要解决两个问题:1) 怎么学习并利用格兰杰因果结构 2) 怎么约束格兰杰因果结构的不变性。首先,针对第一个问题,我们设计出了如下因果数据生成过程。
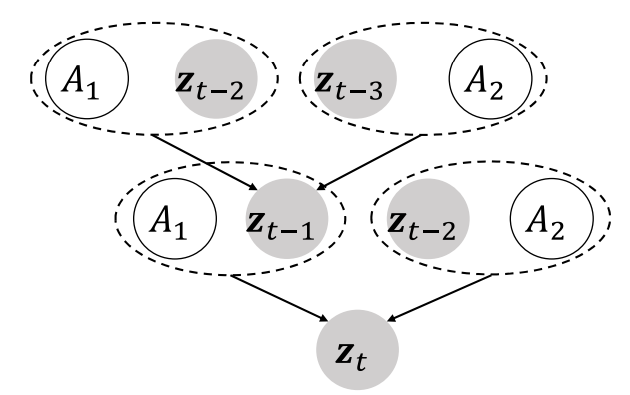
在这个数据生成过程中,表示实验分别为1,2的格兰杰因果结构,表示时间序列不同时刻的值。我们进一步采用变分推断的方法(如理论1所示),来模拟上述因果数据生成过程。

通过理论1, 我们可以通过优化变分上界来发现并利用格兰杰因果结构。基于上述理论,我们可以进一步约束不同领域的格兰杰因果结构的相似性,于是便可以得到如下目标函数:
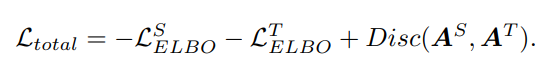
通过上述讨论,我们设计出格兰杰因果对齐模型,如下图所示。
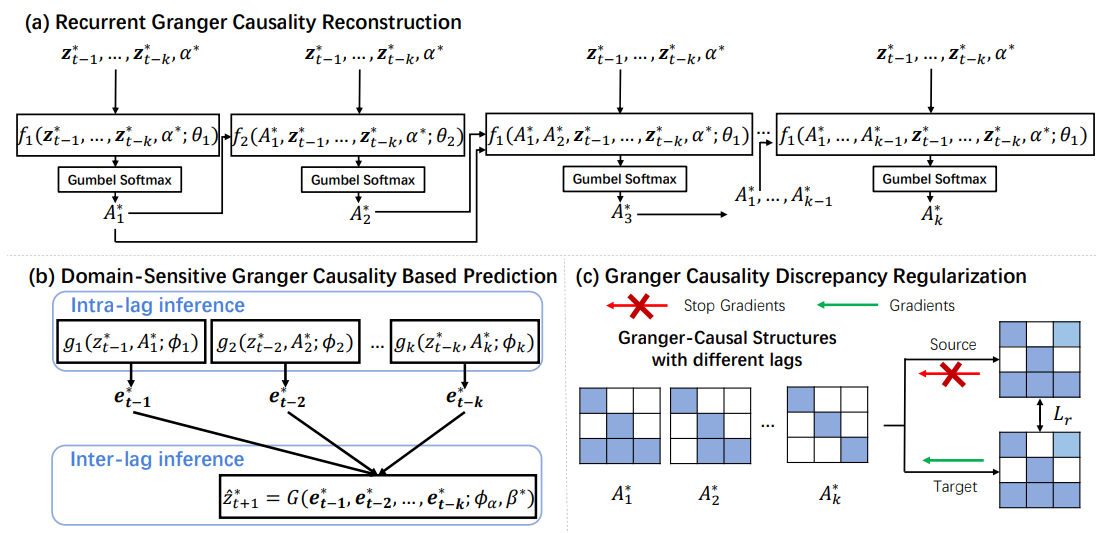
5. 实验结果
在本小节中,我们通过实验结果验证本文提出方法的有效性。首先,我们在模拟数据下验证本方法的有效性(如下图所示)。
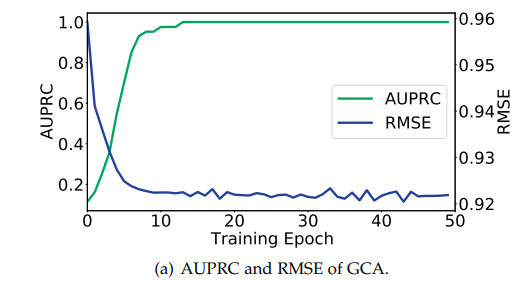
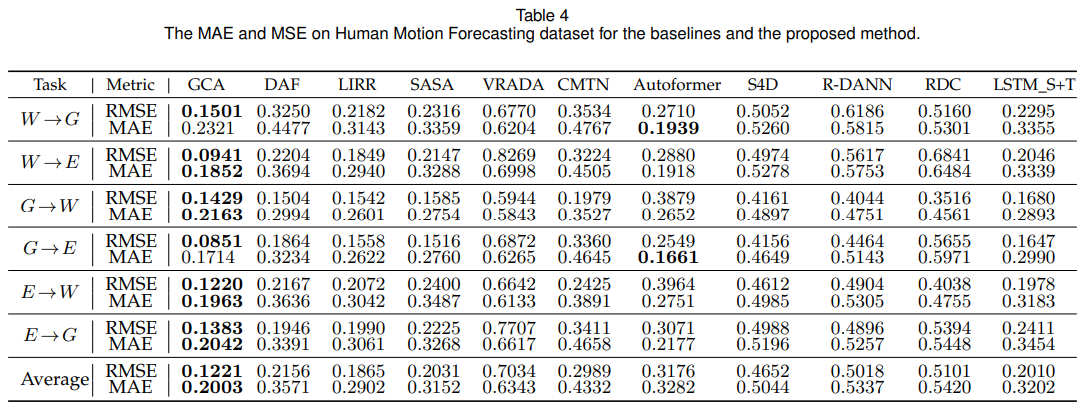
由模拟数据的实验结果,我们可以得出两个结论:1) 本方法可以准确地学习到格兰杰因果结构。2) 只有在格兰杰因果结构学得准确的条件下,本方法才可以获得最优的实验结果。本文进一步在不同的真实数据集(Air Quality Forecasting,空气质量预测数据集, Human Motion Forecasting人体动作预测数据集, PPG-DaLiA人体心跳预测数据集)上验证本方法的实验结果。下图是在人体动作预测数据集上的结果,可以看出本方法在各个迁移方向上都取得了最优的结果。
总结
本文提出了一种半监督时间序列预测的格兰杰因果关系对齐方法。它通过同时发现格兰杰因果关系并基于格兰杰因果结构对时间序列进行预测来进行领域知识的迁移。我们进一步利用格兰杰因果关系差异正则化来放宽因果条件转移的假设。本方法不仅解决了时间序列预测任务中的领域适应问题,还提供了一定程度的可解释性。