导语:近日,广东工业大学计算机学院数据挖掘与信息检索(DMIR)实验室的论文 Exploiting Geometry for Treatment Effect Estimation via Optimal Transport 被CCF A类会议 AAAI 2024 (Association for the Advancement of Artificial Intelligence ) 接收。AAAI 是人工智能领域的顶级会议之一。下面带来该论文的详细解读。

1 研究背景
因果效应估计旨在估计一项策略带来的增量,已广泛应用于现实世界的应用中,例如公共卫生、用户增长等。估计因果效应的理想方法是进行随机对照实验(RCT), 然而,RCT实验通常是昂贵的,甚至是不道德的。因此,如何基于观察数据来估计因果效应是一个十分重要的问题。
基于观察数据估计因果效应的难点是其往往存在混淆偏差,因为观测数据策略分配的非随机性导致了实验组和控制组协变量分布的不平衡。重加权(re-weighting)是减小混淆偏差的有效手段,旨在通过给样本分配新权重以构造协变量分布平衡的伪种群。倾向性得分是计算样本权重的经典方法之一,然而倾向性得分的准确估计很大程度上依赖于策略模型的正确指定,这在复杂的现实世界是不现实的。为了避免这个问题,基于矩条件的方法通过对齐实验组和控制组协变量的矩直接学习样本权重,由于高阶矩的计算仍然是一个富有挑战性的问题,这类方法往往只对齐数据的一阶和二阶矩,但这不足以平衡真实数据的复杂分布,而且很容易被离群点所误导。
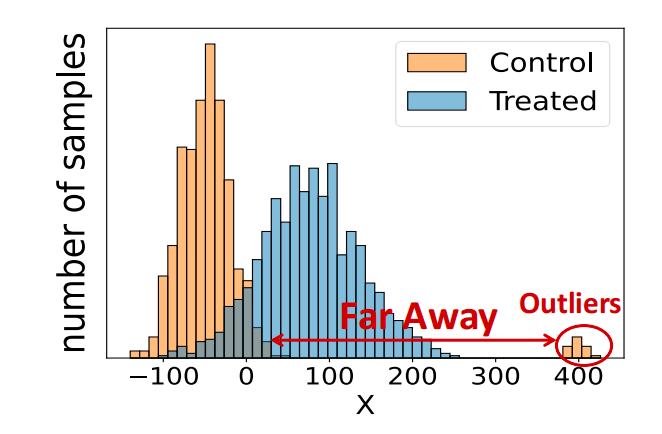
图1展示了基于矩条件的方法被离群点误导的例子。通常来说,离群点的权重应当尽可能小,因为它们不可靠的协变量和结果会给因果效应估计带来负面影响。然而在这个例子中,离群点会被赋予一定程度的权重,因为它们有利于对齐实验组和控制组协变量分布的一阶矩(均值)和二阶矩(方差)。
为了解决上述问题,我们提出通过探索数据中的几何结构信息来学习权重以平衡复杂的协变量分布。具体地,基于最优传输技术,我们提出了施加边缘分布正则约束的 semi-relaxed fused Gromov-Wasserstein 模型来提取数据中蕴含的组间和组内几何结构信息,并提出了一种投影镜像梯度下降法来求解上述问题。
首先,最优传输原问题(KP)和对偶问题(DP)的数学形式分别如下所示:
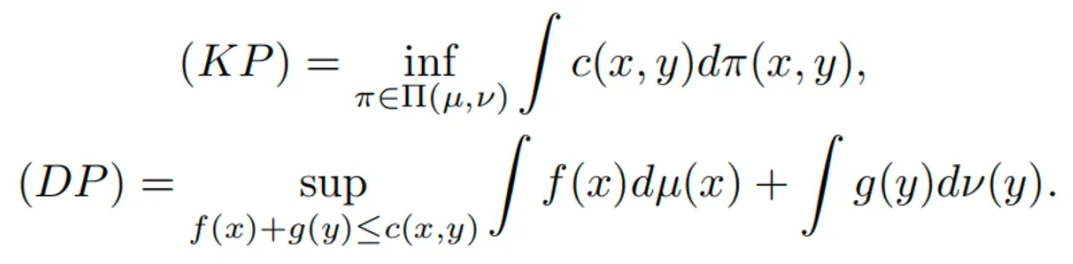
接下来,通过对因果效应估计误差的分解,我们发现其与最优传输的原问题存在以下联系:
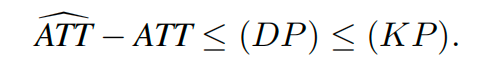
上式说明因果效应估计误差的上界是最优传输的原问题(KP),这从理论上保证了我们能通过最小化KP问题来学习权重,进而使得因果效应估计误差最小。
3 几何结构信息的探索
我们提出如下的施加熵正则约束的 semi-relaxed fused Gromov-Wasserstein 模型来提取数据中蕴含的组间和组内几何结构信息,以学习样本权重来减小混淆偏差:
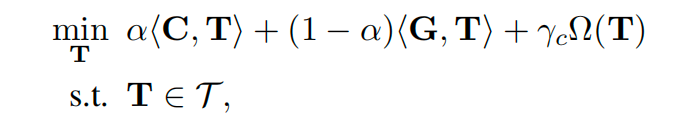
其中,第一项利用了样本组间的几何信息来实现实验组和控制组的分布平衡,因为其倾向于给远离实验组的控制组个体(大的值)赋予小的权重(小的);第二项利用了样本组内的几何信息,根据实验组和控制组中各自样本对的度量信息的相似性进行搬运,以此维持组内几何结构的稳定,同时避免了离群点的干扰;第三项是熵正则化约束,其避免学习到一个稀疏的权重分布,以保证大部分样本被有效利用。
同时,我们提出了一种镜像投影梯度下降算法对上述优化问题进行求解。基于求解得到的最优搬运方案,我们通过下式估计因果效应:
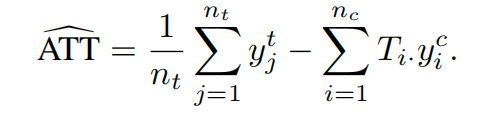
4 实验结果
通过top100权重的可视化验证了本研究提出的OTCI同时探索组间和组内几何结构的必要性(如图2所示),同时在仿真数据和真实数据的实验结果证明了所提出方法的有效性(如表1、表2所示)。
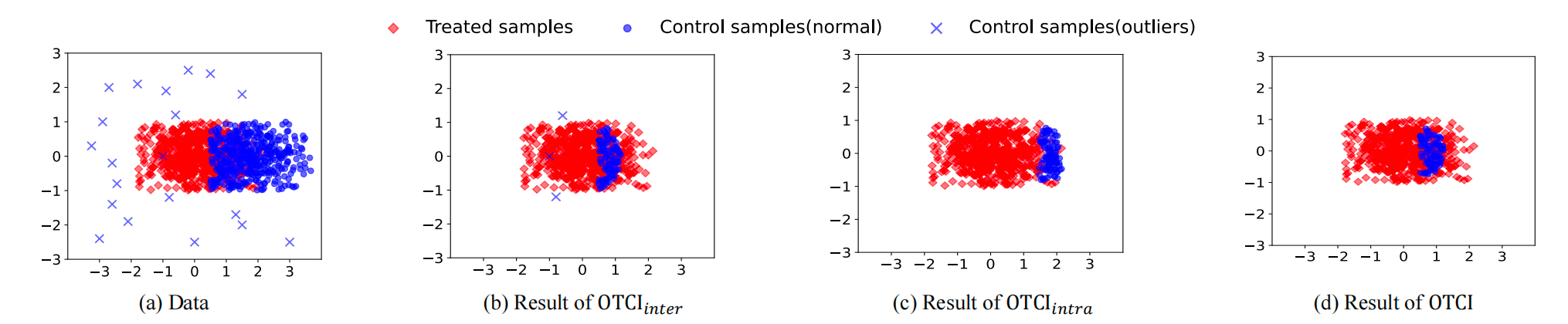
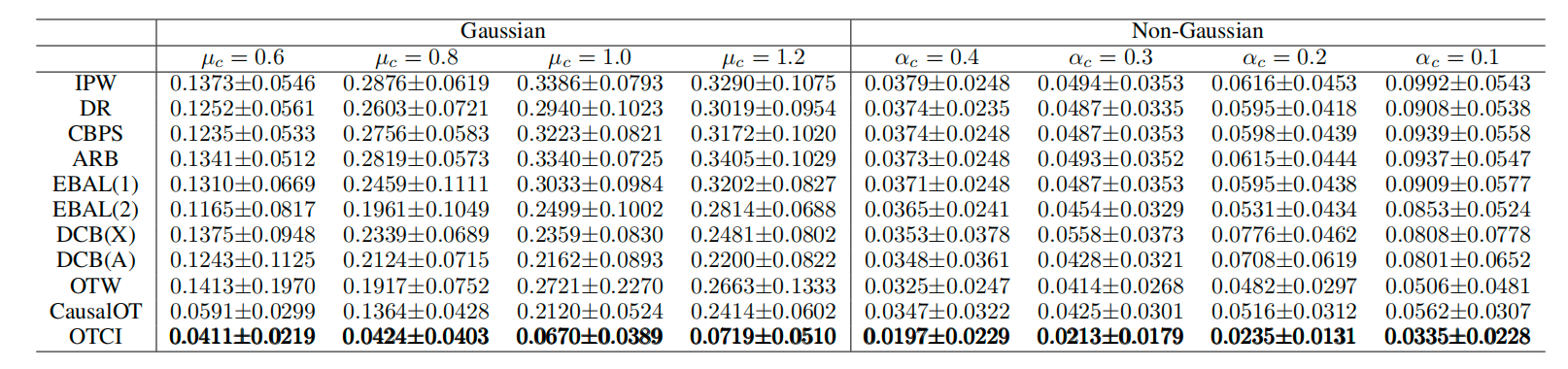
表1 OTCI方法的仿真实验结果
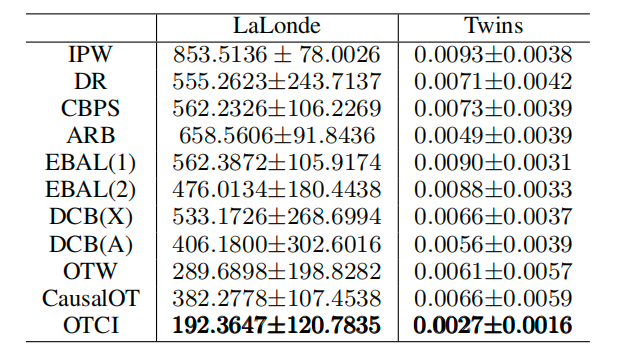
表2 OTCI方法的真实实验结果