导语:近日,广东工业大学计算机学院数据挖掘与信息检索(DMIR)实验室的论文 Testing Conditional Independence Between Latent Variables by Independence Residuals 被 SCI 一区期刊 TNNLS (IEEE Transactions on Neural Networks and Learning Systems) 接收。TNNLS 是人工智能、机器学习、模式识别等多个研究领域的国际顶级期刊。下面带来该论文的详细解读。

1 研究背景
条件独立性检验在多个领域,尤其是因果发现中具有重要作用。然而,大多数现有研究都假设所有被检验的变量是可观测的,然后基于观测数据进行条件独立性检验。然而,实际应用中完全观测所有变量往往是不切实际的。例如,心理健康状态是一组隐变量,通常只能通过问卷测量的观测变量(如抑郁量表)间接获得。在这种情况下,隐变量之间的条件独立性难以直接观测,研究者只能通过这些有限的观测变量获取相关信息。这种部分观测的情况对传统条件独立性检验方法在隐变量因果关系研究中的应用构成了阻碍。因此,迫切需要一种稳健且高效的条件独立性检验方法,以便在部分观测数据下有效应用。
最近的一些研究在一定程度上缓解了这个问题,通常假设每个隐变量都对应一定数量的观测变量。部分方法通过协方差矩阵的秩约束来检验隐变量的条件独立性,但协方差矩阵的秩对估计误差的敏感性影响了其稳健性。另一类方法利用 Gibbs 采样方式估计隐变量的协方差矩阵,再通过偏相关检验隐变量间的条件独立性。然而,基于采样的方法往往计算复杂度高,且依赖难以验证的先验假设,应用受限。
在这一背景下,我们提出了一种基于辅助回归的新方法,用于在线性模型下检验隐变量的条件独立性。我们设计了一种统计可验证的条件独立性检验方法,使得隐变量之间的回归可以利用观测变量完成,从而实现隐变量条件独立性检验。具体而言,我们引入辅助回归过程,通过利用观测变量作为隐变量的替代变量,从而可以推广偏相关检验来判断条件独立性。我们将这一方法命名为基于辅助回归的条件独立性检验(Auxiliary-Regression-based Conditional Independence Test, 简称 AReCI 检验)。通过理论分析和实验验证,AReCI 检验在处理高斯和非高斯数据方面表现出色。此外,我们还发现,经典的偏相关检验可以看作是 AReCI 检验的一种特例。基于 AReCI 检验,我们进一步设计了新的因果发现方法,并在合成数据和真实数据上验证了该方法的有效性,表明其在处理隐变量间的条件独立性检验时具有广泛应用前景。
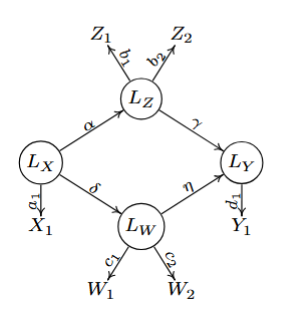
图 1 线性隐变量模型下,一个隐变量间的条件独立性测试的例子
2 基于辅助回归的条件独立性检验(AReCI Test)
本研究在线性模型下,如何测试隐变量间条件独立性关系的问题。在线性模型中,数据的产生过程服从如下结构方程模型:
其中,
指变量
的父母变量集,
是变量
到
的因果效应,
是关于
的噪声项。为了能够检验隐变量间的条件独立性,需要观测变量作为隐变量的代理变量,作为测试隐变量间条件独立性的一种充分条件,如下所示:
条件 1(纯度条件) 每个隐变量至少有两个纯的观测变量作为其孩子变量。
如图1所示,为了测试条件独立性
,需要
满足条件1,即他们存在两个纯的观测孩子变量。在纯度条件下,我们进一步定义隐变量间的辅助回归。
定义1(隐变量的辅助回归)
设
表示一组隐变量,
是满足
的隐变量。在不失一般性的情况下,设
且
可以是
或
,同时
和
是
的两个不相交的观测变量集合,满足
。
在
上的辅助回归定义如下:
其中
是辅助回归的残差,
是从
到其观测变量
的因果强度,
是隐变量
的噪声,
是辅助回归的系数向量,
是噪声项,它是一些观测变量噪声的线性组合。
基于辅助回归,我们可以推广偏相关检验,提出了基于辅助回归的条件独立性测试(Auxiliary-Regression-based Conditional Independence Test),简称AReCI Test。
定义2(AReCI检验)假设数据生成满足线性非循环因果模型并且条件1成立。则给定
的情况下,
和
之间的AReCI检验定义如下:
其中
表示统计独立检验,
是辅助回归的残差,
和
是两个不相交的观测变量集合。如果
则我们认为AReCI检验在情况下成立。
实际上,AReCI Test 的提出,建立在偏相关检验的等价形式的观察上:即偏相关检验可以看成两个回归残差间的独立性检验。基于此,通过构造隐变量间的一种特殊“回归”,并测试该回归残差的独立性,可以检验隐变量间的条件独立性。
我们进一步应用 AReCI Test 于因果关系发现的任务上,提出了一种隐变量因果结构学习的算法,隐变量PC算法。
3 实验结果
在仿真实验上,展示了 AReCI Test 在不同条件集维度下的一类误差(Type I Error)和二类误差(Type II Error)的性能,验证提出工具的有效性,并且将提出的结构学习算法应用于隐变量因果结构学习任务上,验证了提出算法的有效性。
图 2 AReCI Test 条件独立性检验性能仿真实验结果