近日，广东工业大学计算机学院数据挖掘与信息检索(DMIR)实验室的论文Causal Discovery with Latent Confounders Based on Higher-Order Cumulants 被人工智能、机器学习领域的顶级国际会议International Conference on Machine Learning (ICML) 接收。ICML是国际机器学习学会主办的国际会议，也是CCF A 类会议。下面带来该论文的详细解读。
基于高阶统计量的因果网络构建方法
在受到隐变量影响的数据中学习因果结构是一项重要但具有挑战的任务。现有方法大多会假设数据不受到隐变量影响，如线性高斯无环模型。也有假设数据受到隐变量影响，但会认为观测变量之间不存在直接的因果关系。然而，在许多现实世界的应用中，我们可能没有或者不能观测到所有变量，这种变量称为隐变量。其他则称为观察变量。例如我们无法观测到人的心理状况，而人的心理状况会影响到其他的事物。因此，如果忽略了这些隐变量，会导致学习出错误的因果结构。为了解决该问题，本文利用高阶统计量建立了隐变量与观察变量的联系。在此基础上，提出了一种基于高阶统计量的因果结构学习方法，并给出了因果关系的可识别性。该方法在理论分析，与合成数据和真实数据的实验中证明了所提出方法的有效性。
如图1所示，
X1,X2,X3,X4,X5
表示观察变量，L1,L2表示隐变量。观测变量受到隐变量影响是，由于无法从数据中直接找到所有的原因，导致无法识别因果关系。如X1与X2之间受到隐变量L1影响，使得特定因果方向的所独有的独立性无法被检验出来。如X1与X4之间受到隐变量L1影响，使得X1不独立于X4，导致无法识别X1与X4之间不存在直接的因果关系。
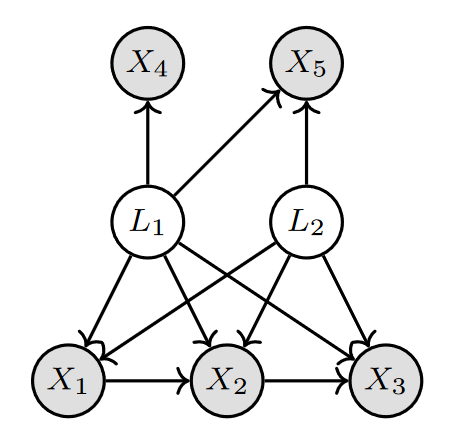
图1 含有隐变量的因果图示例
为了更好地考虑隐变量的影响，本研究通过高阶统计量去挖掘隐变量的信息。具体而言，我们可以通过高阶统计量来刻画隐变量对观察变量的影响：
其中Xi与Xj为观察变量，
为隐变量对观察变量的影响，
为高阶累积量。如果Xi与Xj只受到一个隐变量影响的时候，
就与真实的隐变量对观察变量的影响一致。本研究基于上述结论提出了一个可以检验隐变量方法。并在此基础上，研究了因果结构学习的可识别性条件，进一步提出了一种基于高阶统计量的因果结构学习方法。
所提出的方法在仿真数据和真实数据的实验中均优于其他传统方法（如表1、表2所示），证明了其有效性。
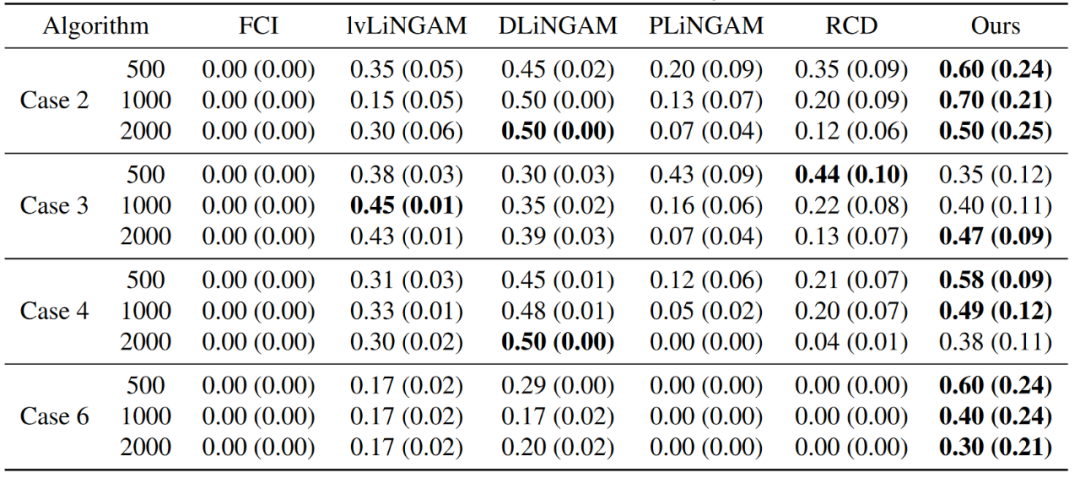
表1 不同方法在识别有向边的F1评分
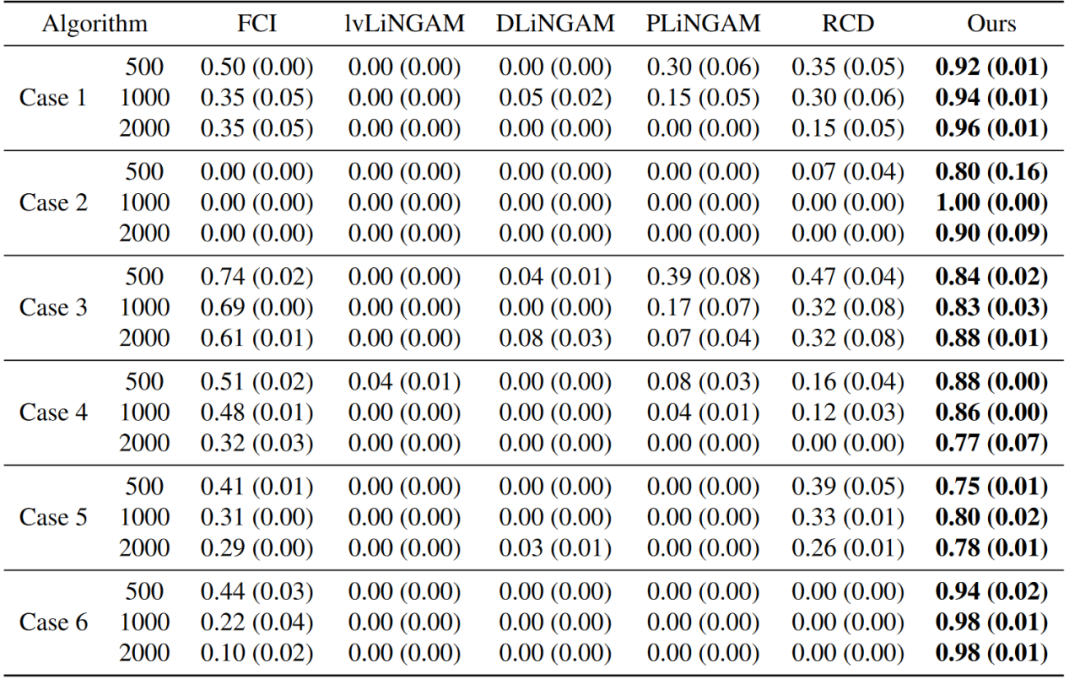
表2 不同方法在识别不存在直接因果关系的F1评分
邮编：510006 地址：广州市番禺区广州大学城广东工业大学工学馆一号馆723室